ความรู้ทั่วไป สารนิเทศ การศึกษา คอมพิวเตอร์ >>

โครงสร้างของคณิตศาสตร์

         คณิตศาสตร์มีบทบาทสำคัญต่อชีวิตของมนุษย์เป็นอันมาก มนุษย์เริ่มเรียนรู้แนวทางคณิตศาสตร์จากสภาพแวดล้อมหรือธรรมชาติแล้วนำไปสู่การสรุปเป็นกฎเกณฑ์ต่าง ๆ ซึ่งสามารถนำไปใช้ประโยชน์ในชีวิตประจำวันได้ คนส่วนใหญ่ที่ไม่ได้เกี่ยวข้องกับคณิตศาสตร์โดยตรงมักจะเข้าใจว่าคณิตศาสตร์เป็นเรื่องของตัวเลขและการคำนวณเท่านั้น ซึ่งที่จริงแล้วคณิตศาสตร์เป็นเรื่องที่หมายรวมไปถึงการแก้ปัญหาและการให้เหตุผลด้วย คณิตศาสตร์นับเป็นเครื่องมือที่สำคัญในการศึกษาค้นคว้าสร้างองค์ความรู้ในศาสตร์อื่น ๆ และคิดค้นสิ่งประดิษฐ์ต่าง ๆ

ดังนั้นในการศึกษาวิชาคณิตศาสตร์จึงจำเป็นจะต้องรู้และเข้าใจเกี่ยวกับธรรมชาติของคณิตศาสตร์เพื่อประโยชน์ในการเลือกวิธีที่จะศึกษาให้เหมาะสมและสอดคล้องกับธรรมชาติของคณิตศาสตร์ต่อไป

1 ธรรมชาติของคณิตศาสตร์

นักการศึกษาทางคณิตศาสตร์ได้สรุปประเด็นธรรมชาติของคณิตศาสตร์ที่สำคัญ ๆ ไว้ดังนี้

คณิตศาสตร์เป็นวิชาที่เกี่ยวกับความคิดรวบยอด

ในวิชาคณิตศาสตร์มีการสร้างความคิดต่าง ๆ ขึ้นซึ่งความคิดเหล่านี้ได้มาจากการสรุปความคิดเห็นที่เหมือน ๆ กัน ซึ่งอาจจะได้จากประสบการณ์หรือปรากฏการณ์ต่าง ๆ ที่เกิดขึ้น เรียกว่า ความคิดรวบยอด เช่น ความคิดรวบยอดเรื่องการเท่ากันของจำนวน รูปสี่เหลี่ยมจัตุรัส การเท่ากันทุกประการ เป็นต้น ซึ่งในแต่ละเนื้อหาของวิชาคณิตศาสตร์เมื่อผู้เรียนได้ศึกษาและจะต้องเกิดความคิดรวบยอดขึ้นในเนื้อหานั้น ๆ จึงจะเกิดประโยชน์

คณิตศาสตร์เป็นวิชาที่แสดงความเป็นเหตุเป็นผล

คณิตศาสตร์เป็นวิชาที่มีการแสดงแนวคิดอย่างเป็นระบบ เป็นขั้นตอน การสรุปในแต่ละขั้นตอนจะต้องมีการอ้างอิงเหตุผลอย่างสมเหตุสมผล ทุกขั้นตอนในแต่ละเนื้อหาจะเป็นเหตุเป็นผลต่อกัน มนุษย์จึงสามารถใช้คณิตศาสตร์เป็นเครื่องมือในการศึกษาค้นคว้าองค์ความรู้ใหม่ ๆ และคิดค้นสิ่งประดิษฐ์ต่าง ๆ ได้

คณิตศาสตร์มีลักษณะเป็นสากล

ในวิชาคณิตศาสตร์จะมีการกำหนดสัญลักษณ์ขึ้นใช้เพื่อสื่อความหมาย ซึ่งทำให้สามารถเขียนข้อความทางคณิตศาสตร์ได้รัดกุม ชัดเจน สื่อความหมายได้ถูกต้อง เกิดความเข้าใจตรงกัน จึงนับได้ว่าคณิตศาสตร์มีภาษาเฉพาะของตัวเอง เป็นภาษาที่ทุกคนที่เรียนคณิตศาสตร์เข้าใจตรงกัน เช่น log 10 = 1 เป็นต้น

คณิตศาสตร์เป็นศิลปะอย่างหนึ่ง

ในการศึกษาวิชาคณิตศาสตร์นั้น นักคณิตศาสตร์นอกจากจะเป็นนักคิดแล้วจำเป็นต้องเป็นผู้มีจิตนาการ ช่างสังเกต มีความละเอียดรอบคอบ รู้จักเลือกคำอนิยาม บทนิยาม สัจพจน์ และทฤษฎีบทมาใช้ได้อย่างถูกต้อง ตามลำดับก่อนหลังพร้อมทั้งการให้เหตุผลอย่างสมเหตุสมผล รวมถึงการถ่ายทอดสิ่งที่พิสูจน์ได้แล้วออกมาอย่างมีระบบระเบียบ เป็นขั้นเป็นตอนอย่างชัดเจน พอจะสรุปได้ว่าความงามของคณิตศาสตร์อยู่ที่ความมีระเบียบ ความกลมกลืนของแนวคิดตลอดจนความละเอียดถี่ถ้วนและรอบคอบ

คณิตศาสตร์เป็นวิชาที่มีโครงสร้าง

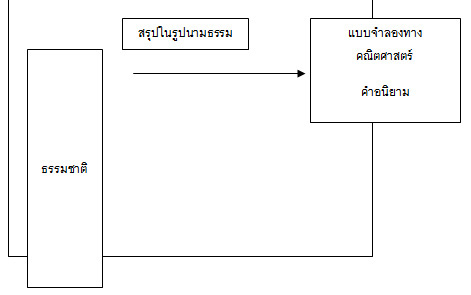
โครงสร้างของคณิตศาสตร์ที่สมบูรณ์นั้นมีกำเนิดมาจากธรรมชาติ โดยมนุษย์ได้เฝ้าสังเกตความเป็นไปของธรรมชาติ ซึ่งอาจจะเป็นทางชีววิทยา ฟิสิกส์ จิตวิทยา เศรษฐศาสตร์ ฯลฯ โดยพิจารณาปัญหาต่าง ๆ ของเนื้อหาเหล่านั้นแล้วสรุปในรูปนามธรรม สร้างแบบจำลองทางคณิตศาสตร์ของเนื้อหานั้น ๆ ซึ่งแบบจำลองทางคณิตศาสตร์ประกอบด้วย คำอนิยาม คำนิยาม และสัจพจน์ จากนั้นจึงใช้ตรรกศาสตร์สรุปออกมาเป็นกฎหรือทฤษฎีบท แล้วนำกฎหรือทฤษฎีบทเหล่านี้ไปประยุกต์ใช้ในธรรมชาติต่อไป ด้วยวิธีการดังกล่าวทำให้มนุษย์เข้าใจความเป็นไปของธรรมชาติได้ดียิ่งขึ้นและในขณะที่นำกฎหรือทฤษฎีบทไปประยุกต์ใช้กับธรรมชาติ อาจจะได้ข้อมูลใหม่ก่อให้เกิดการปรับปรุงแก้ไขแบบจำลอง จนกระทั่งอาจจะ

ทำให้ได้กฎหรือทฤษฎีบทที่ดีกว่าเดิม แล้วนำไปประยุกต์ใช้กับธรรมชาติอีกครั้งหนึ่ง ดังแผนภูมิต่อไปนี้

2 โครงสร้างของคณิตศาสตร์

โครงสร้างของคณิตศาสตร์ประกอบด้วย 4 ส่วน ดังนี้

1. คำอนิยาม คำอนิยาม (undefined term) หมายถึงคำที่ไม่สามารถให้คำจำกัดความได้ แต่สามารถเข้าใจความหมายได้ โดยอาศัยการรับรู้จากประสบการณ์ ความคุ้นเคยกับคุณสมบัติของมัน เช่น จุด เส้น ระนาบ เป็นต้น
2. คำนิยาม คำนิยาม (defined term) หมายถึงคำที่สามารถให้คำจำกัดความได้ เช่น รูปสี่เหลี่ยมจัตุรัส วงกลม เส้นขนาน เป็นต้น
3. สัจพจน์ สัจพจน์ (postulate) หมายถึงข้อความที่ยอมรับหรือตกลงว่าเป็นจริงโดยไม่ต้องพิสูจน์ เช่น “เส้นตรงสองเส้นตัดกันที่จุดเพียงจุดเดียวเท่านั้น” “ลากเส้นตรงให้ผ่านจุดสองจุดที่แตกต่างกันได้เพียงเส้นเดียวเท่านั้น”
4. ทฤษฎีบท ทฤษฎีบท (theorem) หมายถึงข้อความที่สามารถพิสูจน์ได้ว่าเป็นจริง ซึ่งในการพิสูจน์อาจใช้คำอนิยาม คำนิยาม สัจพจน์ หรือทฤษฎีบทอื่น ๆ ที่ได้พิสูจน์มาแล้ว เช่น “มุมภายในรูปสามเหลี่ยมรวมกันเท่ากับ 180 องศา” “เส้นตรงสองเส้นตัดกันมุมตรงข้ามย่อมเท่ากัน”

3 ระบบคณิตศาสตร์

ระบบคณิตศาสตร์มีองค์ประกอบที่สำคัญ 2 ส่วน คือ โครงสร้างของคณิตศาสตร์ และ กระบวนการให้เหตุผล สำหรับโครงสร้างของคณิตศาสตร์ได้กล่าวมาแล้วในหัวข้อ 2 ในหัวข้อ 3 จะกล่าวถึงเฉพาะกระบวนการให้เหตุผล

กระบวนการให้เหตุผล (reasoning) เป็นเครื่องมือที่มนุษย์ใช้แสวงหาความรู้ใหม่ ๆ โดยการนำเอาความจริงอย่างใดอย่างหนึ่งหรือหลายอย่างในระบบ ซึ่งเรียกว่า เหตุหรือข้อตั้ง (premise) มาวิเคราะห์แจกแจงแสดงความสัมพันธ์ เพื่อให้เกิดความจริงอันใหม่ขึ้น ซึ่งเรียกว่า ผล หรือ ผลสรุป หรือ ข้อยุติ (conclusion)

กระบวนการให้เหตุผลแบ่งออกเป็น 2 ลักษณะดังนี้

1. การให้เหตุผลเชิงอุปนัย (inductive reasoning) เป็นการสรุปความรู้ใหม่ หรือสรุปผลการค้นหาความจริง โดยอาศัยข้อสังเกตหรือผลการทดลองหลาย ๆ ตัวอย่าง จากกรณีย่อย ๆ แล้วสรุปเป็นความรู้แบบทั่วไป ซึ่งผลสรุปที่ได้จากการให้เหตุผลแบบนี้ไม่ได้ถูกบังคับจากเหตุที่กำหนดให้ เนื่องจากเหตุแต่ละเหตุที่กำหนดให้หรือนำมาอ้างอิงเป็นอิสระต่อกัน

ตัวอย่าง การให้เหตุผลเชิงอุปนัย
ตัวอย่าง 1 จงหาพจน์ที่ n ของ 1, 3, 5, 7, 9, … พิจารณาแต่ละพจน์ของลำดับต่อไปนี้
พจน์ที่ 1 คือ 1
พจน์ที่ 2 คือ 3 เขียนได้เป็น 1 + 2
พจน์ที่ 3 คือ 5 เขียนได้เป็น 1 + 2 + 2
พจน์ที่ 4 คือ 7 เขียนได้เป็น 1 + 2 + 2 + 2
พจน์ที่ 5 คือ 9 เขียนได้เป็น 1 + 2 + 2 + 2 + 2

จากการสังเกตจะเห็นว่า จำนวนของ 2 ที่บวกกับ 1 น้อยกว่าจำนวนที่แสดงลำดับที่ของพจน์อยู่ 1
ดังนั้นพจน์ที่ 100 คือ 1 บวกด้วย 2 อีก 99 ตัว
นั่นคือ พจน์ที่ 100 คือ 1 + (99 × 2) = 199
ดังนั้น พจน์ที่ n หรือรูปทั่วไปของลำดับ จึงหาได้จาก 1 + (n – 1)2 = 2n – 1
ดังนั้นลำดับ 1, 3, 5, 7, 9, … จึงเขียนเป็น 1, 3, 5, 7, 9, …, 2n – 1

ตัวอย่าง 2 จากการสังเกตต้นมะพร้าวพบว่า
ต้นที่ 1 “ไม่แตกกิ่ง”
ต้นที่ 2 “ไม่แตกกิ่ง”
ต้นที่ 3 “ไม่แตกกิ่ง”
. .
. .
. .
ต้นที่ 100 “ไม่แตกกิ่ง”
จากสิ่งที่สังเกตจึงสรุปว่า “ต้นมะพร้าวทุกต้นไม่แตกกิ่ง”

โดยทั่ว ๆ ไป การให้เกตุผลแบบอุปนัย นิยมใช้ในการศึกษาค้นคว้าคุณสมบัติต่าง ๆ ทางวิทยาศาสตร์ เช่น ข้อสรุปที่ว่า “สารสกัดที่ได้จาดสะเดาสามารถใช้เป็นยากำจัดศัตรูพืชได้” เป็นข้อสรุปที่ได้จากการทดลองซ้ำกันหลาย ๆ ครั้ง แล้วได้ผลการทดลองตรงกัน หรือในทางคณิตศาสตร์จะใช้ในเรื่องการสร้างสัจพจน์ เช่น เมื่อทดลองลากเส้นตรงสองเส้นให้ตัดกัน จะพบว่า เส้นตรงสองเส้นจะตัดกันเพยงจุดเดียวเท่านั้น ไม่ว่าจะทดลองลากกี่ครั้งก็ตาม จึงสรุปได้ว่า เส้นตรงสองเส้นตัดกันเพียงจุดเดียวเท่านั้น

2. การให้เหตุผลเชิงนิรนัย (deductive reasoning) เป็นการสรุปความรู้ใหม่ หรือ ข้อความจริงใหม่ ซึ่งเรียกว่าผลสรุปที่เป็นผลมาจากการนำข้อความที่กำหนดให้ซึ่งยอมรับว่าเป็นจริง ซึ่งเรียกว่าเหตุ ถ้าถ้าเหตุที่กำหนดให้บังคับให้เกิดผลสรุป แสดงว่า การให้เหตุผลดังกล่าวสมเหตุสมผล (valid) แต่ถ้าเหตุที่กำหนดให้ไม่สามารถจะบังคับให้เกิดผลสรุปได้ แสดงว่า การให้เหตุผลดังกล่าว ไม่สมเหตุสมผล (in valid)

ตัวอย่าง การให้เหตุผลเชิงนิรนัย

ตัวอย่าง 3 พิจารณาการให้เหตุผลต่อไปนี้

เหตุ
1. หมูเป็นสัตว์น้ำ
2. สัตว์น้ำทุกชนิดออกลูกเป็นตัว
ผลสรุป หมูออกลูกเป็นตัว

การให้เหตุผลดังกล่าวเป็นการให้เหตุผลที่สมเหตุสมผล เนื่องจากเหตุแต่ละเหตุที่นำมาอ้างอิงบังคับให้เกิดผลสรุป

ตัวอย่าง 4 พิจารณาให้เหตุผลต่อไปนี้

เหตุ
1. มนุษย์ทุกคนมีสองขา
2.ผู้หญิงทุกคนมีสองขา
ผลสรุป ผู้หญิงทุกคนเป็นมนุษย์

จากตัวอย่างนี้จะเห็นว่า ผลสรุปเป็นความจริง แต่เป็นการให้เหตุผลที่ไม่สมเหตุสมผลเพราะเหตุที่นำมาอ้างไม่สามารถบังคับให้เกิดผลสรุปดังกล่าวได้ เหตุแต่ละเหตุมีความเป็นอิสระไม่สัมพันธ์กันแต่ประการใด

คณิตศาสตร์เป็นวิชาที่เกี่ยวกับความคิดรวบยอด มีลักษณะเป็นนามธรรม มีการกำหนดสัญลักษณ์ขึ้นใช้ซึ่งมีลักษณะเป็นภาษาสากล มีความเป็นศิลปะในตัวเอง และมีโครงสร้างที่ชัดเจนซึ่งประกอบด้วย คำอนิยาม คำนิยาม สัจพจน์ และทฤษฎีบท ซึ่งมนุษย์ได้นำคณิตศาสตร์ไปใช้ในชีวิตประจำวัน ตลอดถึงการนำไปใช้ในการประกอบอาชีพต่างๆ

ระบบคณิตศาสตร์ประกอบด้วย โครงสร้างของคณิตศาสตร์ และกระบวนการให้เหตุผลซึ่งเป็นกระบวนการให้เหตุผลเชิงอุปนัย และนิรนัย

อ้างอิง

• วรรณี ธรรมโชติ, ผศ. โครงการตำราวิชาการราชภัฏเฉลิมพระเกียรติ เนื่องในวโรกาสพระบาทสมเด็จพระ
• เจ้าอยู่หัวครองสิริราชสมบัติครบ 60 ปี : หลักการคณิตศาสตร์. กรุงเทพมหานคร : หจก.ภาพพิมพ์, 2550.